Code
ggplot(subcarros, aes(x = date, y = lcar)) +
geom_line(lwd = 0.8, color = "steelblue") +
labs(
subtitle = "Produção de automóveis e comerciais leves",
x = NULL,
y = "Unidades (log)",
caption = "Fonte: BCB") +
theme_bw()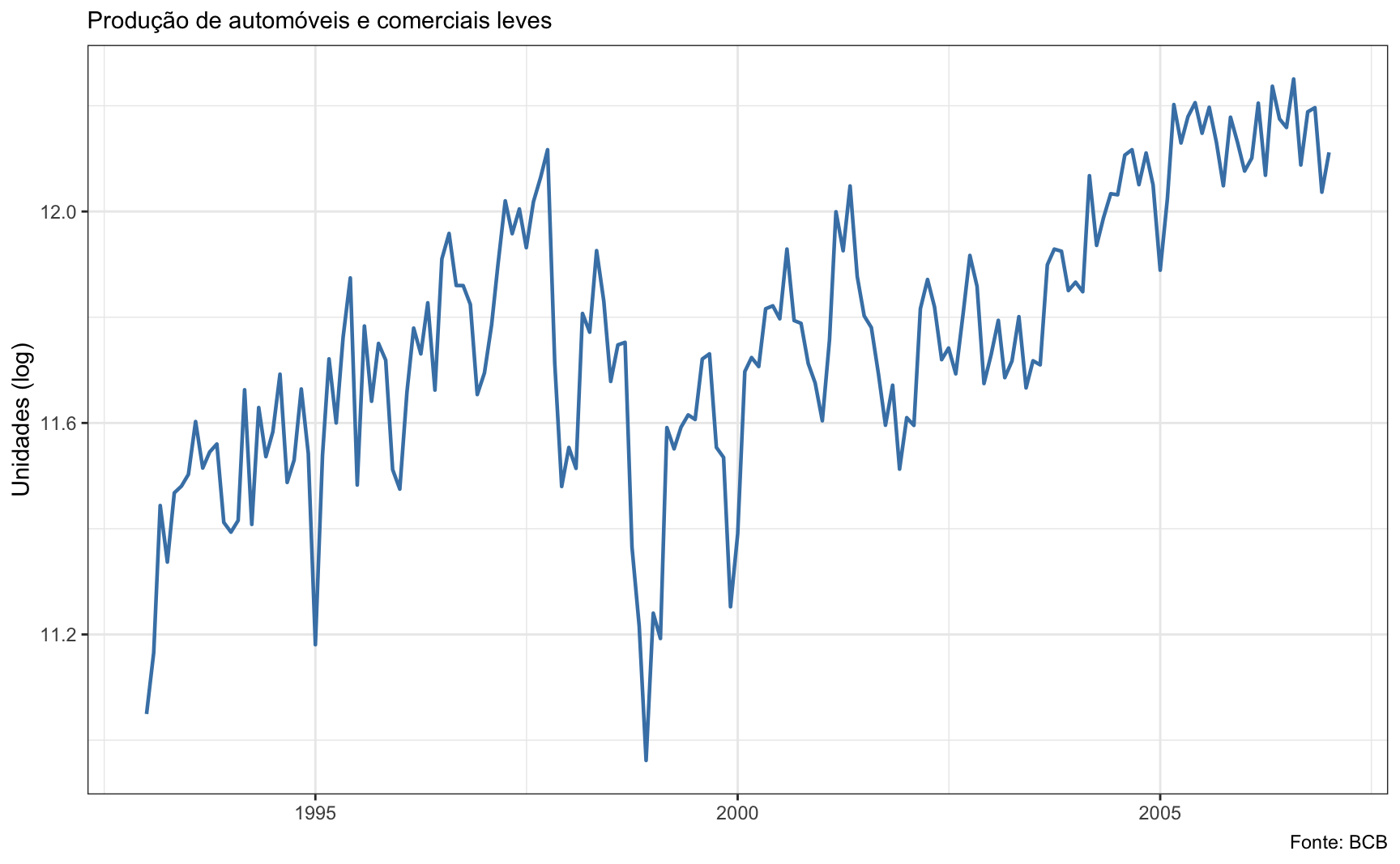
Vinicius Oike
February 14, 2024
Uma tarefa rotineira em pesquisa econômica é de encontrar tendências e ciclos em séries de tempo macroeconômicas. Dada uma série de tempo \(y_t\), tenta-se encontrar alguma decomposição que resulte em:
\[ y_t = \text{cycle}_t + \text{trend}_t + \text{remainder}_t \]
Diferentes teorias e abordagens foram levantadas para extair as tendências de curto e longo prazo de séries.
De maneira geral, há dois tipos de tendências: (1) tendências determinísticas e (2) tendências estocásticas. A forma mais simples de tendência determinística é de uma tendência temporal linear. Algo na forma
\[ y_t = \alpha_{0} + \alpha_{1}t + u_{t} \]
Naturalmente, também é possível propor polinômios de ordem mais elevada para modelar a tendência acima. Contudo, não é usual usar polinômios maiores do que de grau 3, isto é,
\[ y_t = \alpha_{0} + \alpha_{1}t + \alpha_{2}t^2 + \alpha_{3}t^3 + u_{t} \]
Já o exemplo mais simples de série com tendência estocástica é um random-walk
\[ y_t = y_{t-1} + u_{t} \]
A depender do tipo de série que se considera, pode fazer sentido remover diferenças em ordens específicas. Na modelagem SARIMA, por exemplo, tira-se “diferenças sazonais”. No caso de uma série trimestral, por exemplo, pode fazer sentido tirar uma diferença trimestral
\[ z_{t} = y_{t} - y_{t-4} \]
O gráfico abaixo mostra a produção de automóveis no Brasil entre 1993 e 2007. Os dados são da Anfavea e baixados no R via API do Banco Central. A série não foi ajustada sazonalmente.

O painel abaixo mostra as séries sem tendência e o gráfico de autocorrelação do resíduo do ajuste. Note que é possível perceber visualmente a presença de uma componente sazonal que permanece na série. Os resíduos do ajuste com polinômio de terceiro grau ainda apresentam bastante autocorrelação, sugerindo que a série não é tendência-estacionária. O ajuste na primeira diferença parece ser mais adequado neste caso.
p1 <- ggplot(subcarros, aes(x = date, y = resid_tt)) +
geom_line(lwd = 0.8, color = "steelblue") +
geom_hline(yintercept = 0) +
labs(x = NULL, title = "Tendência cúbica") +
scale_y_continuous(limits = c(-0.5, 0.5)) +
theme_bw()
p2 <- ggplot(subcarros, aes(x = date, y = resid_sto)) +
geom_line(lwd = 0.8, color = "steelblue") +
geom_hline(yintercept = 0) +
scale_y_continuous(limits = c(-0.5, 0.5)) +
labs(x = NULL, title = "Tendência estocástica I(1)") +
theme_bw()
p3 <- ggAcf(ts(subcarros$resid_tt, frequency = 12), lag.max = 84) +
ggtitle("ACF: resíduos tendência cúbica") +
scale_y_continuous(limits = c(-0.5, 0.5)) +
theme_bw()
p4 <- ggAcf(ts(subcarros$resid_sto, frequency = 12), lag.max = 84) +
ggtitle("ACF: resíduos tendência I(1)") +
scale_y_continuous(limits = c(-0.5, 0.5)) +
theme_bw()
(p1 + p2) / (p3 + p4)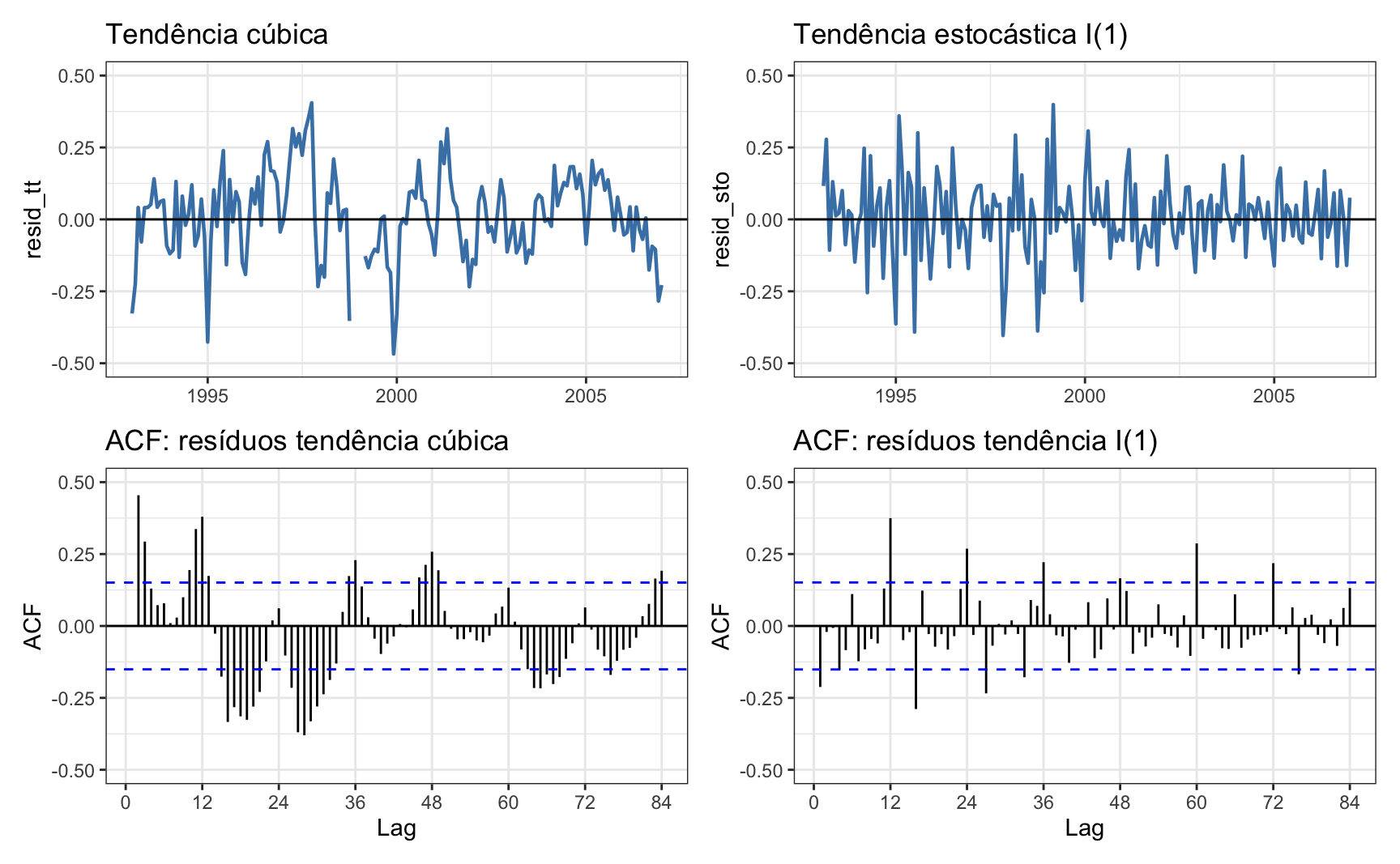
Uma abordagem bastante comum para encontrar a tendência/ciclo em séries macroeconômicas é o filtro Hodrick-Prescott (HP). O filtro HP separa uma série em suas componentes de tendência e ciclo. Sua formulação matemática baseia-se na minimização de uma função objetivo que busca encontrar uma estimativa suave da tendência subjacente, ao mesmo tempo em que penaliza variações abruptas.
Dada uma série temporal \(y_t\), o objetivo é encontrar uma tendência \(g_t\) que minimize a seguinte função objetivo:
\[ \min_{g_t} \left[ \sum_{t=1}^{T} \left( y_t - g_t \right)^2 + \lambda \sum_{t=2}^{T-1} \left( g_{t+1} - 2g_t + g_{t-1} \right)^2 \right] \]
O primeiro termo representa a soma dos quadrados dos resíduos entre a série observada e a estimativa da tendência, enquanto o segundo termo é uma penalidade que desencoraja variações abruptas na tendência. O filtro HP suaviza a série observada, permitindo identificar movimentos de longo prazo enquanto remove flutuações de curto prazo. O parâmetro \(\lambda\) desempenha um papel crucial na determinação do nível de suavização da tendência, com valores maiores resultando em tendências mais suaves.
Note que se \(\lambda = 0\) o valor ótimo de \(g_{t}\) é simplesmente \(y_{t}\). Quando \(\lambda \to \infty\) o componente \(g_{t}\) se aproxima de uma tendência temporal linear. A escolha de \(\lambda\) não é simples e é usual amparar-se em regras de bolso. Para séries trimestrais, costuma-se usar \(\lambda = 1600\); para séries mensais \(\lambda = 14400\)1.
Apesar de ter sido desenvolvida para séries macroeconômicas, não há problema, em princípio, em aplicar o filtro HP a qualquer tipo de série. O gráfico abaixo mostra o resultado da aplicação do filtro HP à série de produção de veículos.
y <- ts(log(subcarros$value), frequency = 12)
hpy <- hpfilter(y, freq = 14400, type = "lambda")
tbl_hp <- tibble(
date = as.numeric(time(y)),
trend = as.numeric(hpy$trend),
series = as.numeric(y)
)
ggplot(tbl_hp, aes(x = date)) +
geom_line(aes(y = series), lwd = 0.8, color = "#023047") +
geom_line(aes(y = trend), lwd = 0.8, color = "#ffb703") +
labs(subtitle = "Filtro HP: Série e Tendência", x = NULL, y = NULL) +
theme_bw()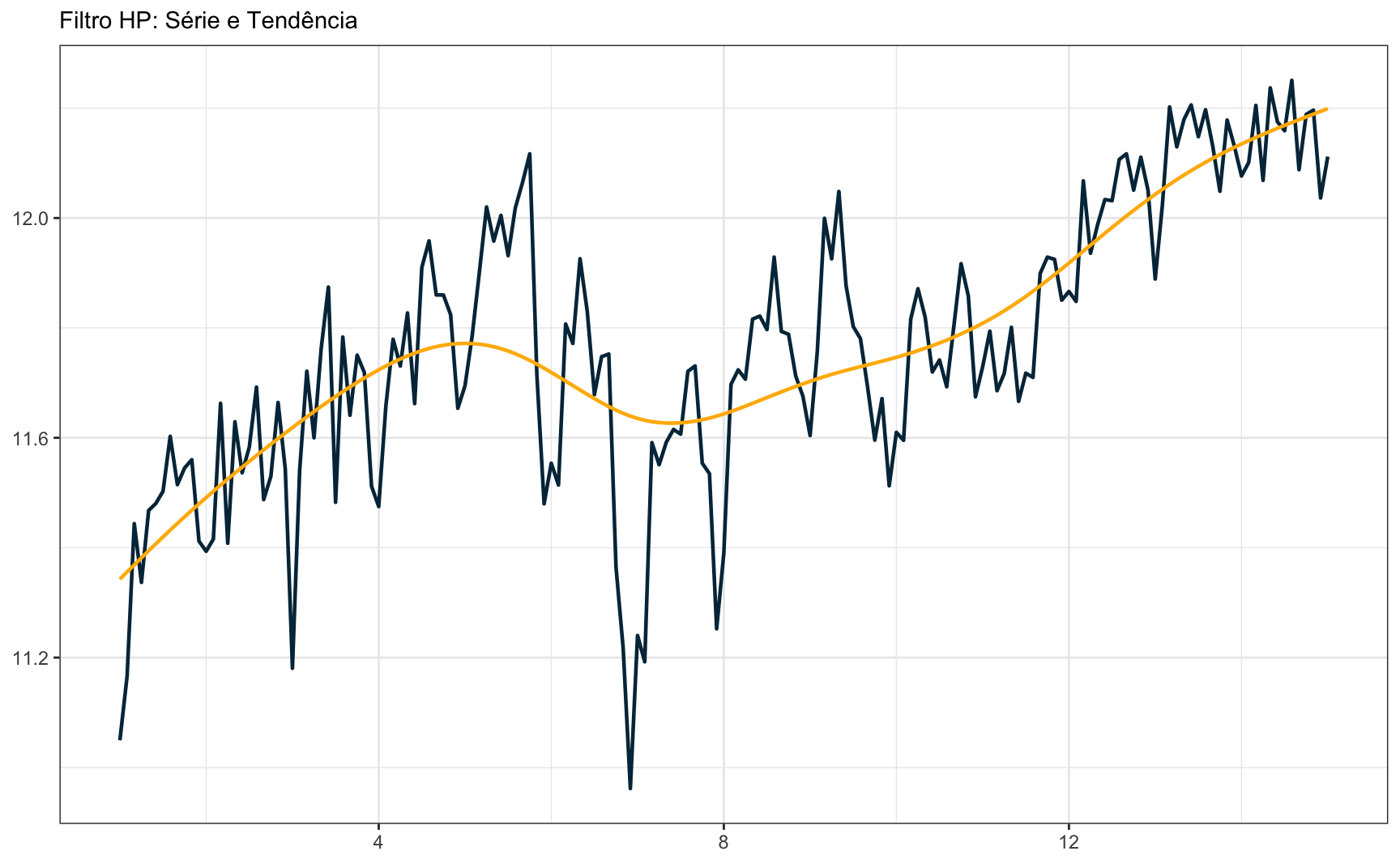
O passeio aleatório é um processo estocástico comum em economia. Variáveis importantes como preços futuros, preços de ações, preços de petróleo, conusmo, inflação, e a taxa de crescimento do estoque de moeda podem ser modeladas como passeios aleatórios.
Seja um passeio aleatório \((1-L)y_{t} = u_{t}\) com \(T\) observações e frequência trimestral, onde \(L\) é o operador defasagem usual: \(Lx_{t} = x_{t-1}\). Segundo Hamilton (2017), Quando se aplica o filtro HP sobre \(y_{t}\) encontra-se o seguinte termo de ciclo, \(c_t\)
\[ c_{t} = \frac{\lambda(1-L)^3}{F(L)}u_{t+2} \]
Usando \(\lambda = 1600\), a sugestão usual para séries trimestrais,
\[ c_t = 89.72 \{ - q_{0,t+2} + \sum^{\infty}_{j=0} (0.8941)^j[\cos(0.1117j)+8.916\sin(0.1117j)](q_{1,t+2-j} + q_{2,t+2+j}) \} \]
onde
\(q_{0t} = \varepsilon_t - 3\varepsilon_{t-1} + 3\varepsilon_{t-2} - \varepsilon_{t-3}\)
\(q_{1t} = \varepsilon_t - 3.79\varepsilon_{t-1} + 5.37\varepsilon_{t-2} - 3.37\varepsilon_{t-3} + 0.79\varepsilon_{t-4}\)
\(q_{2t} = -0.79\varepsilon_{t+1} + 3.37\varepsilon_t - 5.37\varepsilon_{t-1} + 3.79\varepsilon_{t-2} - \varepsilon_{t-3}\)
que é uma expressão bastante longa. O importante a se notar é que o termo \(c_{t}\) tem uma estrutura recursiva em função das defasagens de \(\varepsilon_t\). Note que a série subjacente é simplesmente uma soma de ruídos aleatórios sem nenhum padrão:
\[ \begin{align} (1-L)y_{t} & = \varepsilon_{t} \\ y_{t} & = \frac{\varepsilon_{t}}{(1-L)} \\ y_{t} & = \sum_{i = 0}^{\infty}e_{i} \end{align} \]
mas o ciclo desta série tem uma estrutura artifical, que foi acrescentada pelo uso do filtro HP. Em linhas gerais, a exposição acima resume o argumento de Hamilton contra o uso indiscriminado do filtro HP em séries macroeconômicas não-estacionárias. O filtro HP acaba “criando” uma estrutura nos dados que não existia previamente.
set.seed(1984)
y <- ts(cumsum(rnorm(100)), frequency = 4)
hpy <- hpfilter(y, freq = 1600, type = "lambda")
tbl_hp <- tibble(
date = as.numeric(time(y)),
cycle = as.numeric(hpy$cycle),
trend = as.numeric(hpy$trend),
series = as.numeric(y)
)
p1 <- ggplot(tbl_hp, aes(x = date)) +
geom_line(aes(y = series), lwd = 0.8, color = "#023047") +
geom_line(aes(y = trend), lwd = 0.8, color = "#ffb703") +
labs("Filtro HP aplicado no Random Walk", subtitle = "Série e Tendência", x = NULL, y = NULL) +
theme_bw()
p2 <- ggplot(tbl_hp, aes(x = date)) +
geom_line(aes(y = cycle), lwd = 0.8, color = "#023047") +
labs(x = NULL, y = NULL, subtitle = "Ciclo") +
theme_bw()
p1 / p2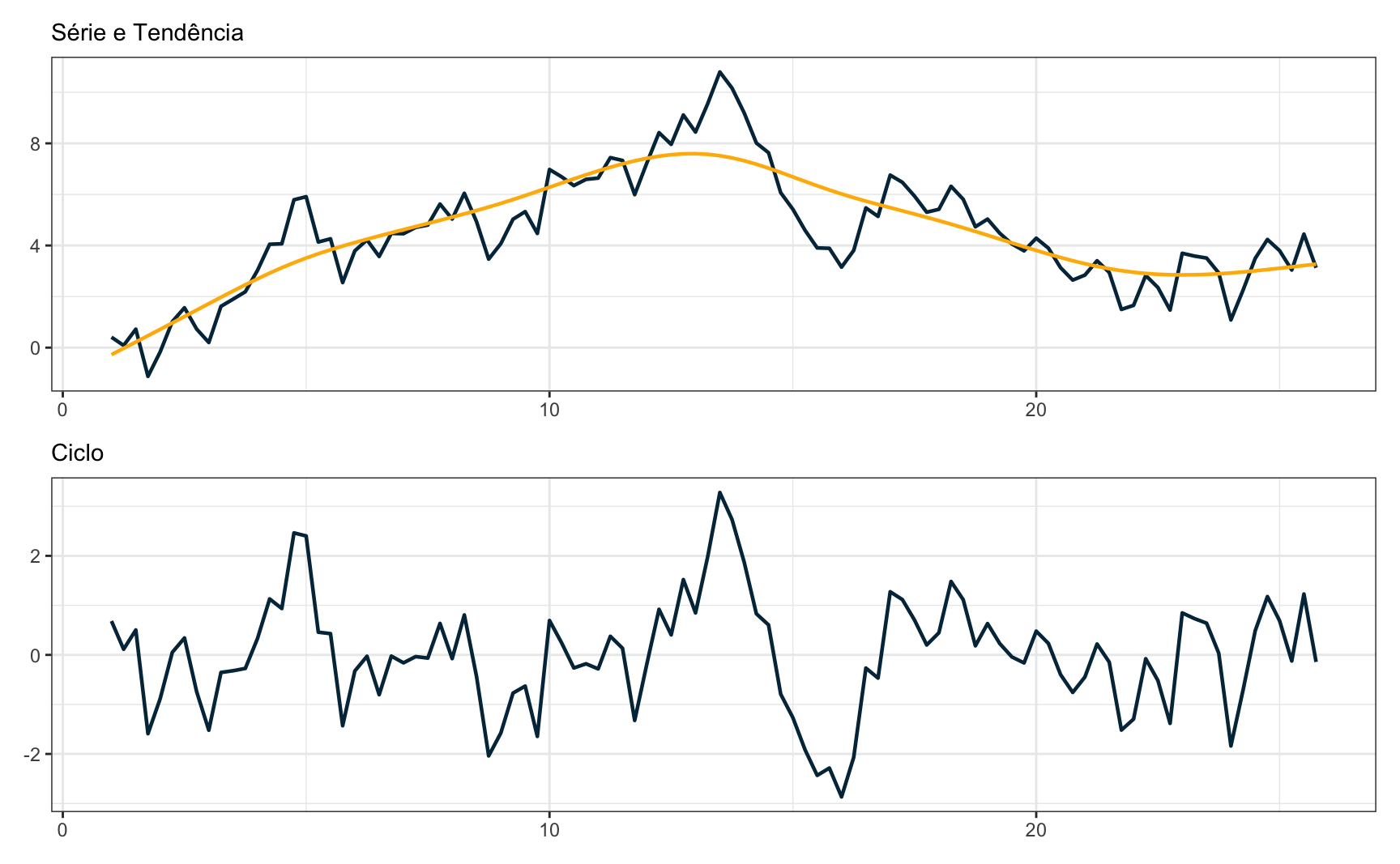
Para um exemplo mais aplicado, vamos usar a base USMacroG do pacote {AER}. O código abaixo aplica o filtro HP sobre o logaritmo das séries trimestrais do PIB, consumo, investimento e M1. As séries são todas completas com 204 observações entre 1950 e 2000.
O gráfico mostra o ajuste do filtro HP em cada uma das quatro séries.
library(AER)
data("USMacroG")
macro <- tibble(
date = zoo::as.Date.ts(USMacroG),
as.data.frame(USMacroG)
)
macro <- macro |>
mutate(across(gdp:m1, log))
nest_macro <- macro |>
select(date, gdp, consumption, invest, m1) |>
pivot_longer(col = -date, names_to = "name_series") |>
group_by(name_series) |>
nest()
macro_hp <- nest_macro |>
mutate(hpy = map(data, \(x) {
y <- ts(x$value, frequency = 4, start = c(1950, 1))
hp <- hpfilter(y, freq = 1600, type = "lambda")
tibble(
cycle = as.numeric(hp$cycle),
trend = as.numeric(hp$trend)
)
})) |>
unnest(c(data, hpy)) |>
ungroup()
p1 <- ggplot(macro_hp, aes(x = date, y = value)) +
geom_line(aes(y = value), lwd = 0.8, color = "#023047") +
geom_line(aes(y = trend), lwd = 0.8, color = "#ffb703") +
facet_wrap(~name_series, scales = "free_y", ncol = 1) +
labs(x = NULL, y = NULL)+
theme_bw()
p2 <- ggplot(macro_hp, aes(x = date, y = cycle)) +
geom_line(lwd = 0.8, color = "#023047") +
geom_hline(yintercept = 0) +
facet_wrap(~name_series, ncol = 1) +
labs(x = NULL, y = NULL) +
theme_bw()
p1 + p2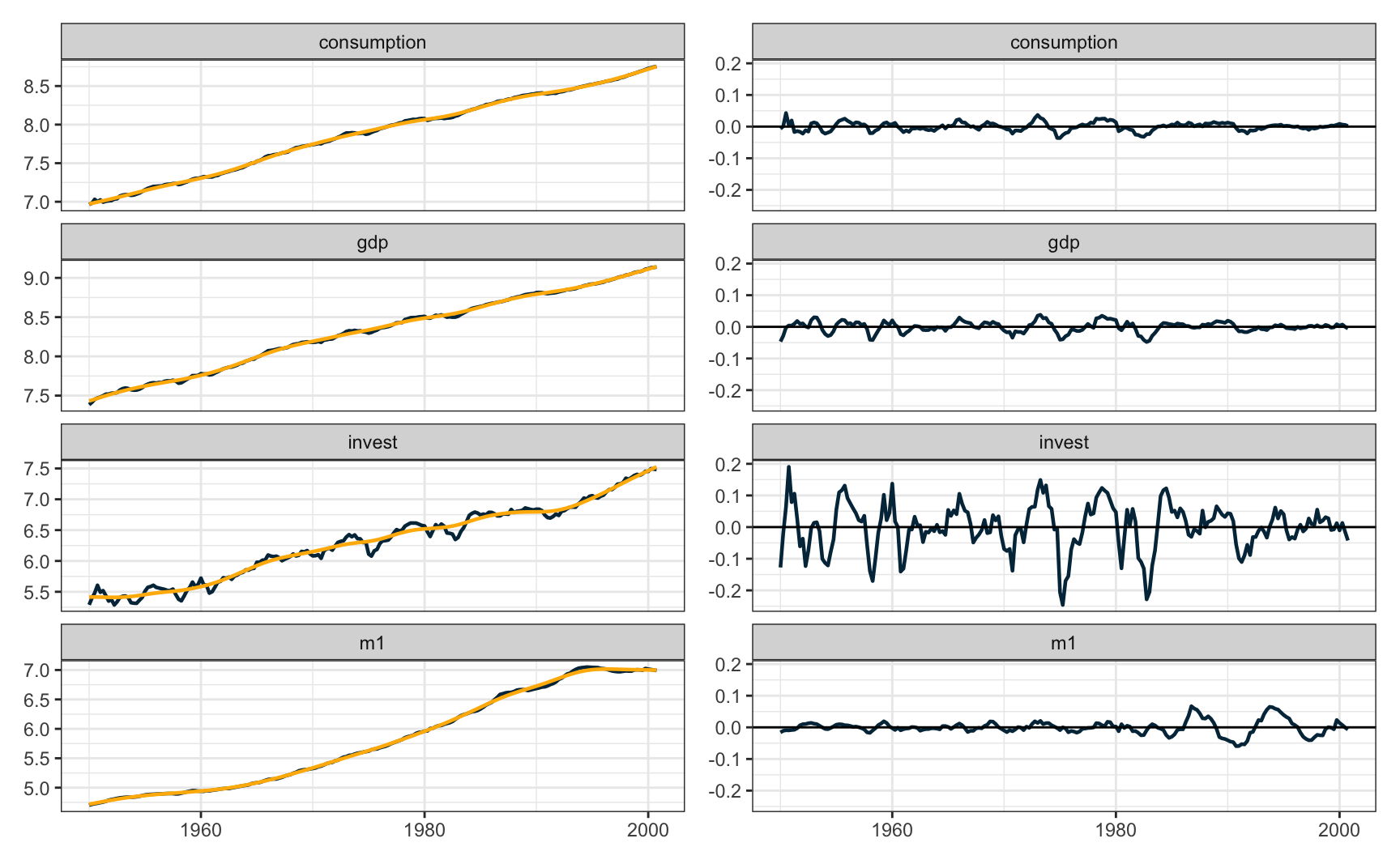
A análise das autocorrelações mostra que há bastante autocorrelação cruzada entre as séries.
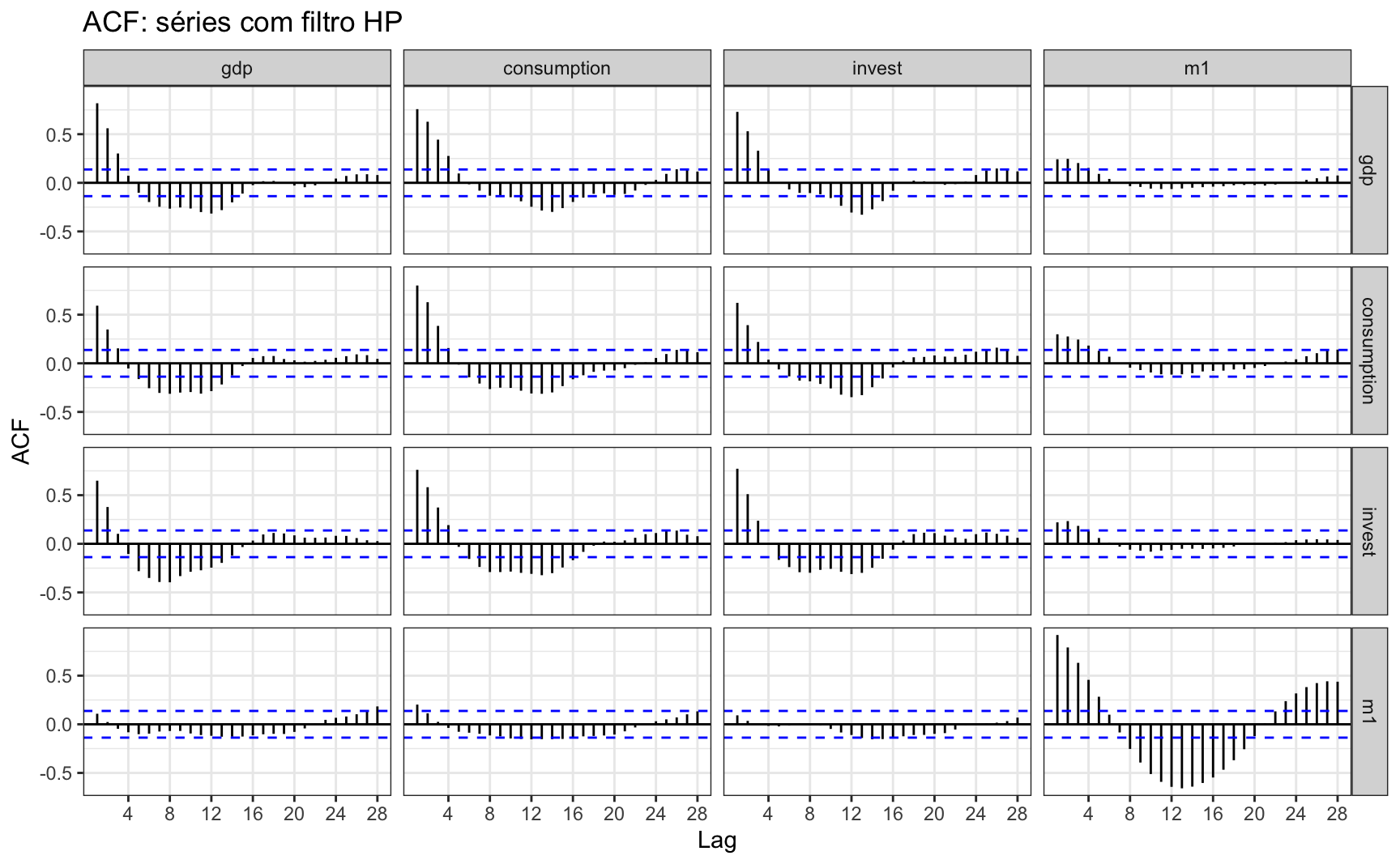
Se tivéssemos assumido, contudo, que as séries são I(1), não haveria muita correlação cruzada entre as séries.
Como alternativa ao filtro HP Hamilton (2017) sugere um procedimento bastante simples. Seja \(y_t\) uma série não-estacionária. Então fazemos uma regressão linear de \(y_{t+h}\) contra os \(p\) valores mais recentes.
\[ y_{t+h} = \beta_0 + \beta_{1} y_{t} + \beta_{2} y_{t-1} + \beta_{3} y_{t-2} + \beta_{4} y_{t-3} + u_{t+h} \]
Para o caso específico de dados trimestrais, ele sugere uma formulação do tipo:
\[ y_{t} = \beta_0 + \beta_{1} y_{t-8} + \beta_{2} y_{t-9} + \beta_{3} y_{t-10} + \beta_{4} y_{t-11} + u_{t+h} \]
Ou, alternativamente, um modelo ainda mais simples, em função apenas de \(y_{t-8}\) na forma:
\[ y_{t} = \beta_0 + \beta_{1} y_{t-8} + u_{t+h} \]
De modo geral, Hamilton argumenta que este filtro garante a estacionaridade de séries, sendo elas tendência-estacionárias ou diferença-estacionárias. Mais detalhes sobre o filtro podem ser verificados no Working Paper.
O primeiro passo necessário é preparar os dados. Novamente, vamos trabalhar com as séries num padrão retangular, usando um tibble. A base de dados utilizada é a USMacroG, descrita acima; neste caso, vamos adicionar as séries de gasto do governo e inflação. Isto é, temos agora seis séries: PIB, consumo, investimento, gasto do governo, inflação e M1. Todas as variáveis, exceto pela taxa de inflação, serão transformadas usando log, seguindo o paper de Hamilton.
O código abaixo tem um trecho interessante onde se usa uma combinação de map e partial para criar várias colunas com os valores defasados das variáveis.
data(USMacroG)
macro <- tibble(
date = zoo::as.Date.ts(USMacroG),
as.data.frame(USMacroG)
)
macro_long <- macro |>
select(date, gdp, consumption, invest, m1, government, inflation) |>
mutate(across(gdp:government, ~log10(.x) * 100)) |>
pivot_longer(-date, names_to = "name_series")
macro_lags <- macro_long |>
group_by(name_series) |>
mutate(
across(value,
map(1:12, ~partial(dplyr::lag, n = .x)),
.names = "l{.fn}")
)Hamilton sugere duas maneiras de tirar a tendência dos dados: usando uma regressão linear e tirando uma diferença simples. No caso de séries trimestrais, o autor sugere \(p=4\) e \(h=8\). Assim, temos de estimar um modelo linear da forma:
\[ y_{t} = \beta_0 + \beta_{1} y_{t-8} + \beta_{2} y_{t-9} + \beta_{3} y_{t-10} + \beta_{4} y_{t-11} + u_{t+h} \]
E a série livre de tendência, \(z_t\) será dada por:
\[ z_{t} = y_{t} - \hat{\beta_0} - \hat{\beta_1}y_{t-8} - \hat{\beta_2}y_{t-9} - \hat{\beta_3}y_{t-10} - \hat{\beta_4}y_{t-11} \]
No segundo “modelo”, vamos simplesmente tirar uma diferença na forma:
\[ z_{t} = y_{t} - y_{t-8} \]
O primeiro modelo será chamado de “regression”, enquanto o segundo modelo será chamado de “Random Walk”. O código abaixo faz a regressão em todas as séries e grava os resultados do fit e os resíduos de todos os modelos.
Idealmente, deve-se verificar o comportamento dos resíduos do modelo de regressão. Neste caso, estes resíduos são considerados o componente cíclico da série original. O painel abaixo mostra os resíduos da primeira série, do PIB. O gráfico de cima é simplesmente o gráfico do resíduo. No gráfico inferior-esquerdo temos o gráfico de autocorrelação da série e no gráfico inferior-direito temos o historgrama dos resíduos com a densidade da distribuição normal superimposta.
Vale lembrar que não estamos buscando limpar a série totalmente de autocorrelação, como na modelagem ARIMA.
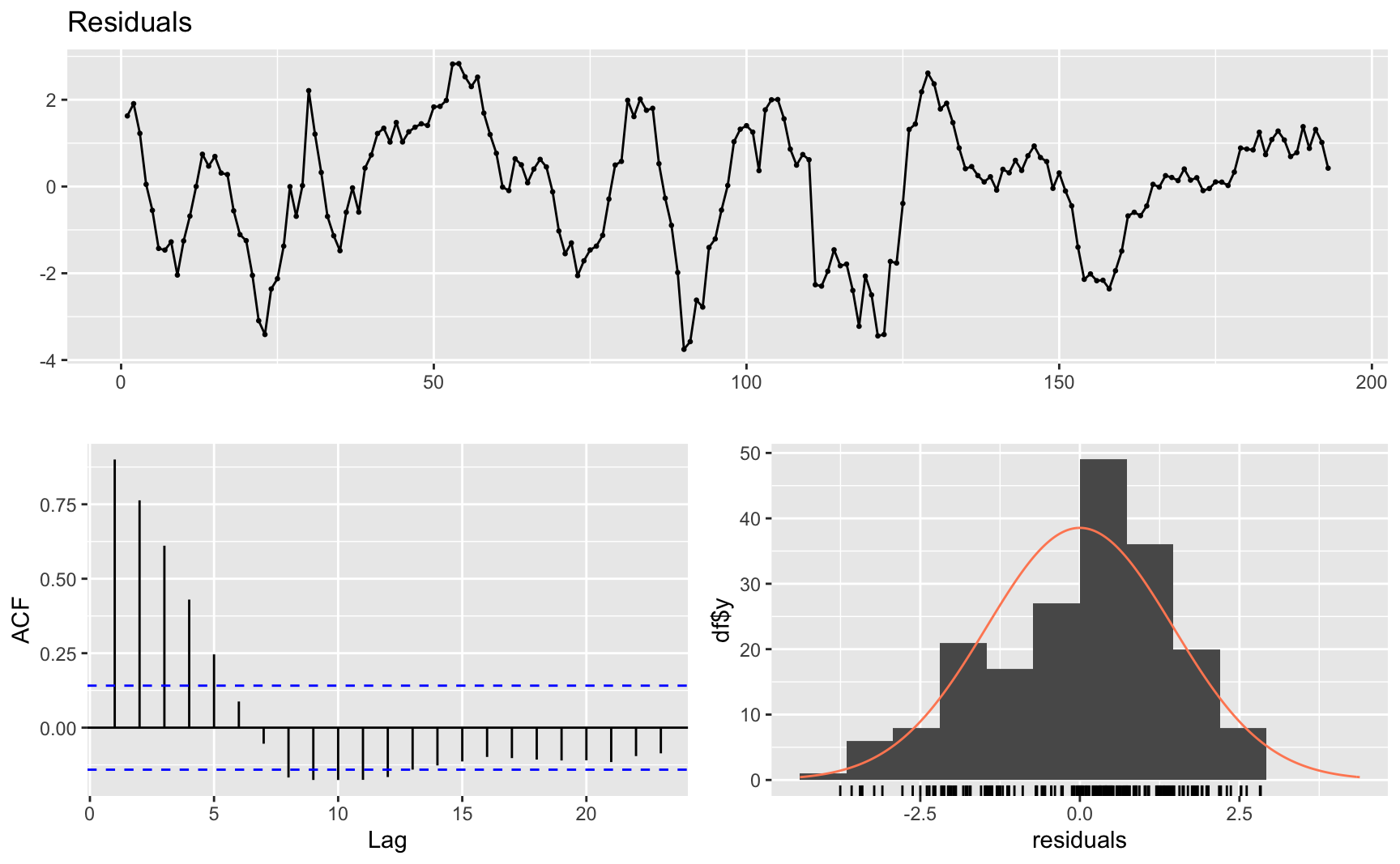
Ljung-Box test
data: Residuals
Q* = 417.09, df = 10, p-value < 2.2e-16
Model df: 0. Total lags used: 10NULLEvidentemente, não é fácil inspecionar os resíduos de todos os modelos, especialmente quando o número de séries é muito grande. O painel abaixo mostra o gráfico de autocorrelação entre as seis séries consideradas. Na diagonal principal temos o gráfico do resíduo da própria série; nos demais gráficos, mostra-se a autocorrelação cruzada entre os resíduos.
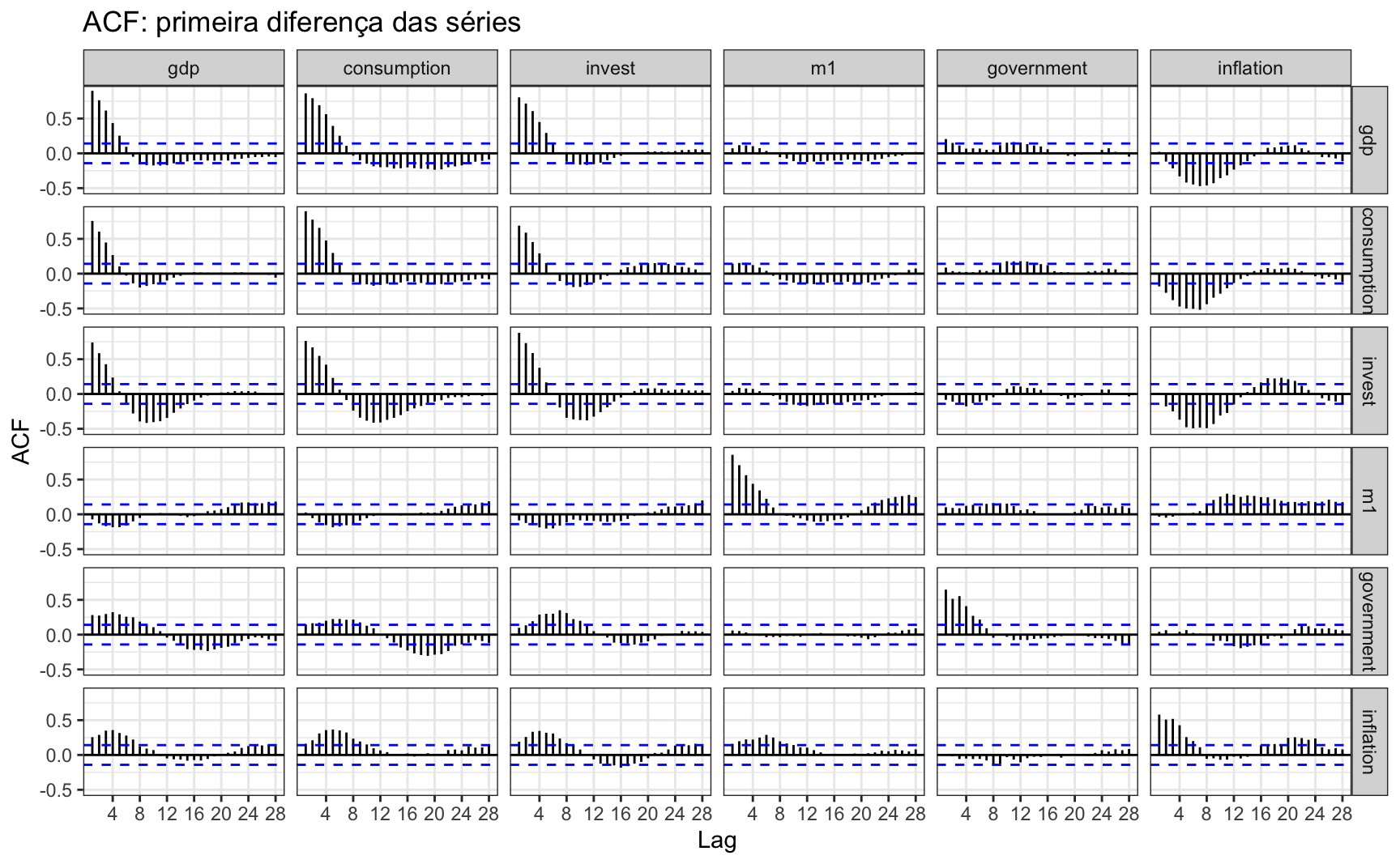
O código abaixo junta todas as séries para facilitar a sua visualização. Como há várias séries e muita repetição, crio uma função plot_series para facilitar a construção dos painéis.
m1 <- macro_models |>
ungroup() |>
select(name_series, trend, resid) |>
unnest(cols = c("trend", "resid")) |>
mutate(id = as.numeric(names(trend)), .before = everything())
macro_trend <- macro_models |>
select(name_series, data) |>
unnest(cols = c(data)) |>
mutate(id = vctrs::vec_group_id(date), .before = everything()) |>
ungroup()
macro_trend <- macro_trend |>
left_join(m1, by = c("id", "name_series"))
series_trend <- macro_trend |>
select(date, name_series, trend, resid, resid_rw) |>
pivot_longer(cols = -c(date, name_series), names_to = "name_decomp") |>
mutate(decomp = if_else(str_detect(name_decomp, "trend"), "trend", "resid")) |>
filter(!is.na(value))
plot_series <- function(x, ylim = c(NA, NA)) {
p1 <- ggplot() +
geom_line(
data = dplyr::filter(series_trend, name_series == x, decomp == "trend"),
aes(x = date, y = value),
lwd = 0.8,
color = "steelblue"
) +
labs(x = NULL, y = NULL) +
ggtitle(glue::glue("Series: {x}")) +
theme_bw() +
theme(plot.title = element_text(size = 10))
p2 <- ggplot() +
geom_hline(yintercept = 0) +
geom_line(
data = dplyr::filter(series_trend, name_series == x, decomp == "resid"),
aes(x = date, y = value, color = name_decomp),
lwd = 0.8
) +
scale_x_date(
breaks = seq(as.Date("1950-01-01"), as.Date("2000-01-01"), by = "10 year"),
date_labels = "%Y"
) +
scale_y_continuous(limits = ylim) +
scale_color_manual(
name = "",
values = c("#003049", "#d62828"),
labels = c("Regression", "Random Walk")) +
labs(x = NULL, y = NULL) +
ggtitle(glue::glue("Cyclical Component: {x}")) +
theme_bw() +
theme(legend.position = "top", plot.title = element_text(size = 10))
return(list(trend = p1, cycle = p2))
}O gráfico abaixo mostra o ajuste do filtro de Hamilton nas séries de PIB e de consumo.
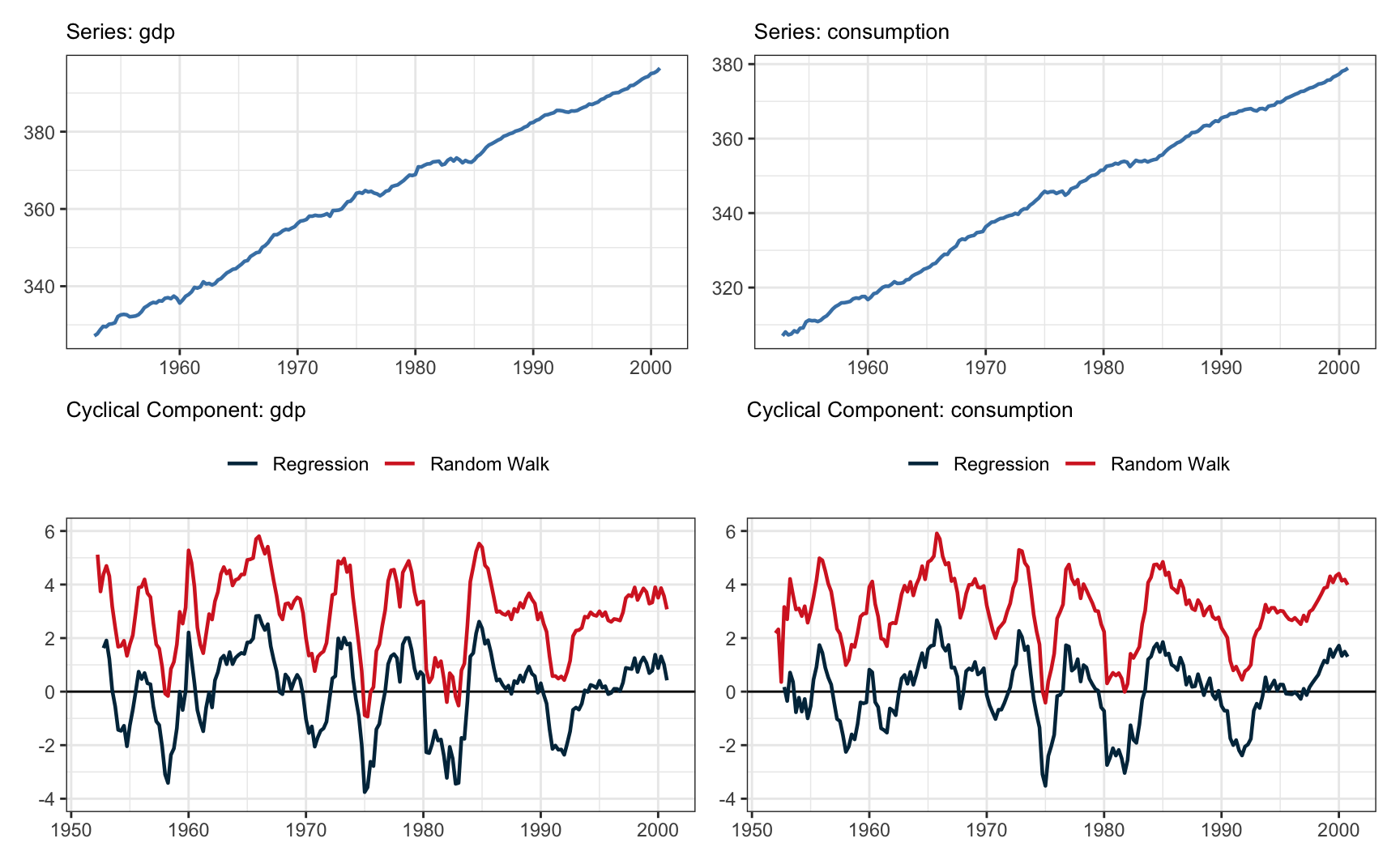
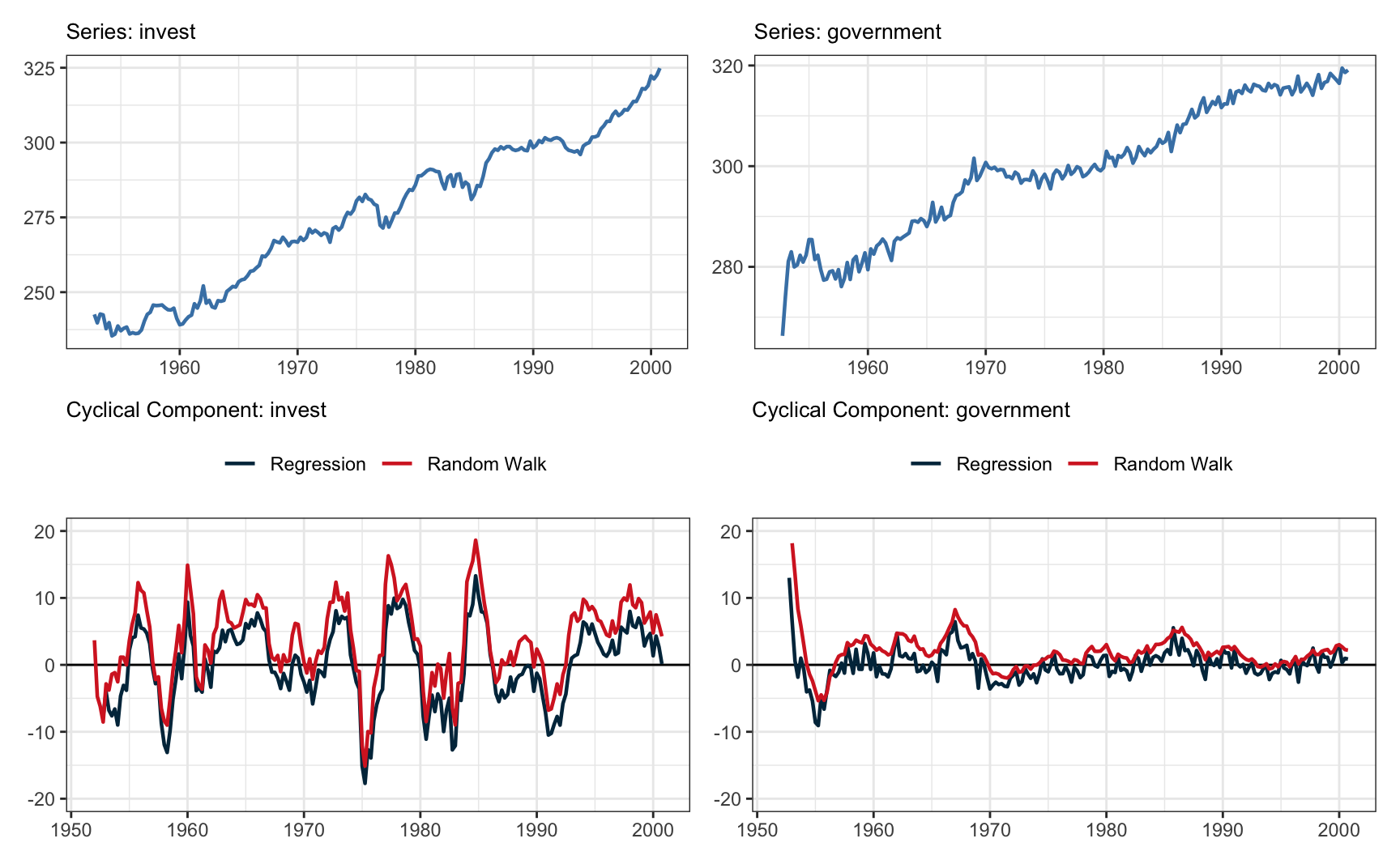
O gráfico abaixo mostra o ajuste do filtro de Hamilton nas séries de investimento e gasto do governo.
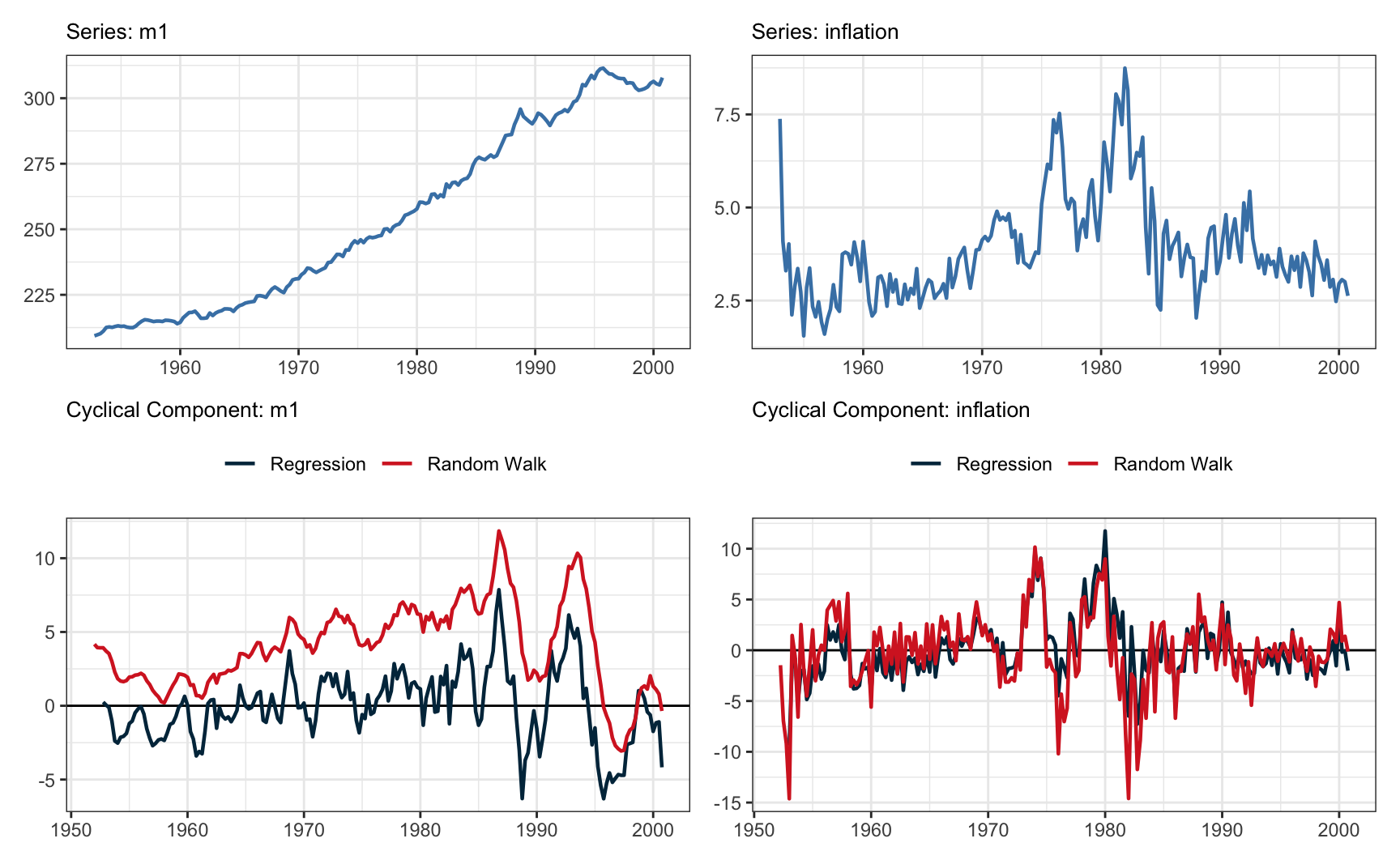
Finalmente, o gráfico abaixo mostra o ajuste do filtro de Hamilton nas séries de M1 e de inflação.
O filtro proposto por Hamilton tem diversas características interessantes. A simplicidade e intuição do filtro, em especial, são pontos atrativos. Um paper recente, de Viv Hall e Peter Thompson (2021), contudo, não encontrou grandes vantagens deste filtro em relação aos tradicionais filtro HP e filtro Baxter-King. Os autores testam os filtros usando um amplo conjunto de séries macroeconômicas da Nova Zelândia. De maneira geral, o filtro de Hamilton gerou séries com maior volatilidade e pior capacidade preditiva. Considerando a literatura de filtros, parece improvável, de fato, que um filtro tão simples possa ter uma melhor performance do que filtros no domínio da frequência.
Para uma discussão sobre a escolha de \(\lambda\) em séries macroeconômicas, veja Ravn e Uhlig (2002)↩︎